Пусть один из пучков, достаточно разреженный и однородный по сечению, состоит из одинаковых частиц с массами , движущихся с одинаковыми импульсами . Второй пучок, также разреженный и однородный по сечению, состоит из других одинаковых частиц с массами и импульсами .

Процесс рассеяния одного пучка на другом, ввиду их разреженности, можно свести к рассеянию каждой частицы одного пучка на некоторой частице другого пучка и рассмотреть, таким образом, независимые акты рассеяния разных пар частиц. Рассеяние каждой пары характеризуется своим прицельным расстоянием и происходит в определенной плоскости относительно системы центра масс пары.

Центры масс всех пар взаимодействующих частиц покоятся относительно друг друга, поскольку эти пары движутся с одинаковой скоростью относительно л-системы. Поэтому угол рассеяния для каждой пары частиц в ее системе центра масс будет одним и тем же относительно системы отсчета с началом в центре масс любой пары. Последнюю условно будем называть системой центра масс или ц-системой.

Важной характеристикой процесса рассеяния является дифференциальное эффективное поперечное сечение рассеяния. Для описанной выше картины рассеяния эта величина определяется как отношение числа частиц пучка, рассеиваемых в элемент телесного угла за единицу времени, к числу частиц того же пучка, пролетающих за единицу времени через единичную площадку поперечного сечения пучка до рассеяния¹.

Дифференциальное сечение рассеяния обозначается и по определению равно

Кроме дифференциального сечения часто рассматривают полное эффективное сечение рассеяния. Оно равно отношению общего числа частиц данного пучка, рассеиваемых за единицу времени под всеми углами, к плотности потока этого пучка до рассеяния:

В силу центральной симметрии взаимодействия частиц соответствующие рассматриваемым парам -точки, прицельные расстояния которых лежат внутри интервала , а плоскости движения имеют все возможные ориентации относительно импульса -точек до рассеяния, рассеются на углы каждая в своей плоскости и на достаточном удалении от начала ц-системы попадут в телесный угол (см. Рис. 6.4). Этот телесный угол ограничен поверхностями конусов с вершинами в начале ц-системы и углами растворов, равными соответственно и . Ось конусов параллельна импульсу -точек до рассеяния. Частицы первого пучка, соответствующие рассмотренным -точкам, после рассеяния попадут в этот же телесный угол , поскольку они движутся по траекториям, подобным траекториям -точек и с теми же импульсами. Частицы второго пучка рассеются в телесный угол той же величины, но с растворами конусов, направленными в противоположную сторону.

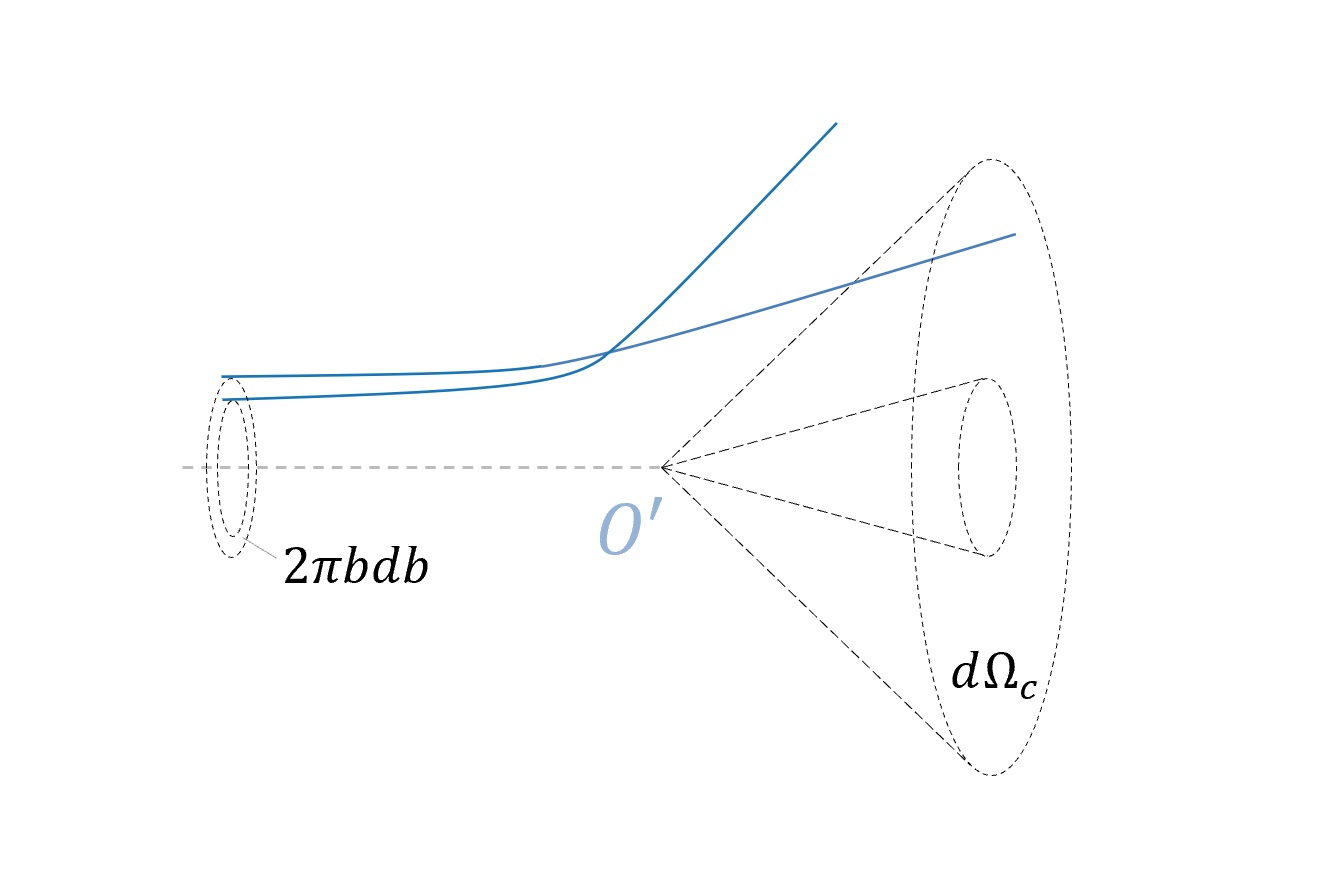
Рис. 6.4 Траектории -точек, соответствующих разным парам взаимодействующих частиц, с прицельными расстояниями и всеми возможными ориентациями плоскостей движения относительно импульса -точек до рассеяния

Поскольку до рассеяния пучки однородны по сечению, поток числа частиц с прицельными расстояниями равен плотности потока частиц до рассеяния, умноженной на площадь кольца с радиусами . Тогда число частиц, рассеиваемых в элемент телесного угла за единицу времени, равно

Откуда можно получить дифференциальное сечение рассеяния частиц первого и второго пучков в системе центра масс как функцию прицельного расстояния:

Дифференциальное сечение рассеяния обоих пучков в системе центра масс как функция угла рассеяния

где прицельное расстояние как функция угла и относительного импульса частиц (или их относительной кинетической энергии) до рассеяния получается разрешением уравнения относительно . Элемент телесного угла .

Дифференциальные сечения рассеяния частиц первого и второго пучков в лабораторной системе отсчета можно получить как результат подстановок

Углы и – углы рассеяния частиц первого и второго сортов в л-системе. При рассеянии первой частицы на второй покоящейся зависимости и без особых принципиальных трудностей определяются с помощью импульсных диаграмм (см. Раздел III, Рассеяние двух частиц. Импульсные диаграммы).

В случае двузначной зависимости угла рассеяния частицы в ц-системе от угла ее рассеяния в л-системе дифференциальное сечение рассеяния есть сумма дифференциальных сечений по однозначным ветвям указанной функции.

Введенное понятие дифференциального эффективного сечения рассеяния позволяет описать рассеяние частиц пучка неподвижной мишенью (см. Рис. ). Нетрудно видеть, что при однократном рассеянии число частиц пучка с плотностью потока , рассеянных мишенью с концентрацией рассеивателей в элемент телесного угла за единицу времени, есть произведение дифференциального сечения рассеяния частиц на плотность потока пучка и число рассеивателей в объеме мишени, ограниченном поперечным сечением пучка до рассеяния. То есть,

где – площадь пятна пучка на мишени до рассеяния, – толщина мишени в направлении первоначального падения пучка.

>>Контрольные вопросы и задания

Классическая задача рассеяния двух частиц <<

1. Величина носит название плотности потока параллельного моноэнергетического пучка.